Total derivative corrige erro comum na backpropagation em deep learning
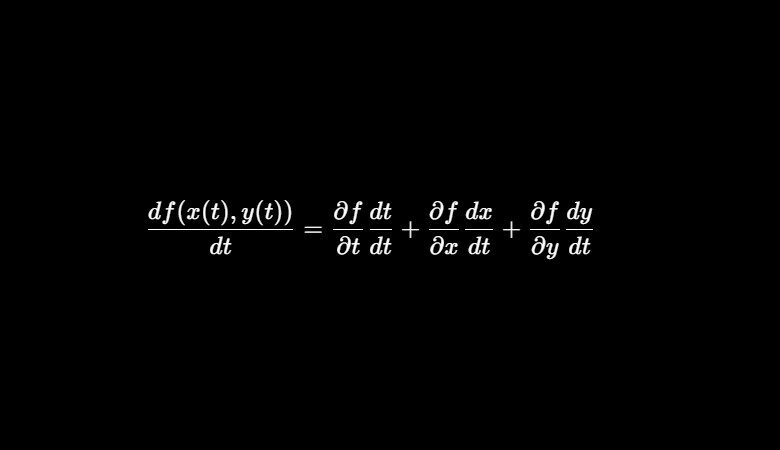
São Paulo — InkDesign News —
Um artigo recente detalha nuances matemáticas essenciais para o entendimento correto da backpropagation em redes neurais, um pilar dos métodos de machine learning e deep learning. A abordagem destaca o uso apropriado da derivada total e do vector chain rule para derivar os gradientes durante o treinamento, corrigindo confusões comuns na área.
Arquitetura de modelo
A backpropagation envolve o cálculo do gradiente da função de custo em relação aos pesos de uma rede neural, buscando minimizar o erro durante o treinamento. Na passagem direta, cada neurônio realiza uma soma ponderada das entradas seguida da aplicação de uma função de ativação, produzindo um vetor de saídas para a camada. A arquitetura utiliza matrizes de pesos para representar a conexão entre camadas, e o vetor saída é transformado de forma afim, com não linearidades aplicadas para modelagem de fenômenos complexos.
“A saída de uma camada pode ser vista como uma função vetorial que mapeia uma entrada em um vetor de saída, cuja dimensionalidade depende do número de neurônios da camada.”
(“Each layer in a neural net can be seen as a vector function that receives a vector of inputs and maps (transforms) them to an output vector. The dimensionality of the output vector is determined by the number of neurons in that layer.”)— Autor do artigo, Toward Data Science
Treinamento e otimização
Ao calcular os gradientes para cada camada, a derivada total é necessária especialmente nas camadas ocultas, pois os pesos influenciam indiretamente a saída e, consequentemente, o custo final. A formulação matemática utiliza o vector chain rule, que generaliza a regra da cadeia para múltiplas variáveis e permite o cálculo eficiente via multiplicação matricial das jacobianas. Importante salientar que, para a última camada, não é preciso a derivada total, mas sim a regra da cadeia simples estendida para vetores.
“A derivada do custo em relação às ativações da última camada é calculada aplicando a regra da cadeia estendida para vetores, evitando a complexidade introduzida pela derivada total, que é necessária somente para as camadas ocultas.”
(“The derivative of the cost with respect to the activations of the final layer is calculated by applying the vector-extended chain rule, avoiding the complexity introduced by the total derivative, which is necessary only for hidden layers.”)— Autor do artigo, Toward Data Science
Esta estrutura matemática permite a pré-computação de certos gradientes reutilizáveis, como o gradiente da soma ponderada em relação aos pesos, que é simplesmente o vetor de ativações da camada anterior. Tais simplificações são cruciais para acelerar o treinamento, especialmente em redes profundas e com grandes volumes de dados.
Resultados e métricas
Implementações práticas, como a realizada em código numpy com o conjunto de dados Iris, demonstram a eficácia do método para calcular gradientes que suportam a minimização da função de custo via gradiente descendente. Com a correta aplicação da derivada total e do vector chain rule, obtém-se gradientes precisos que garantem o ajuste eficiente dos pesos da rede.
O insight matemático minimiza os erros conceituais existentes em explicações superficiais e otimiza a performance computacional. O uso da função ReLU para camadas ocultas, por exemplo, possibilita derivadas simples que facilitam o cálculo dos gradientes.
“A derivada da função ReLU é uma matriz de 1s e 0s, dependendo do sinal da entrada, o que torna a computação do gradiente eficiente e direta durante a retropropagação.”
(“The derivative of the ReLU function is a matrix of 1s and 0s, depending on the sign of the input, which makes the computation of the gradient efficient and straightforward during backpropagation.”)— Autor do artigo, Toward Data Science
Estes avanços matemáticos vão além da teoria ao fornecer bases sólidas para o desenvolvimento de modelos mais complexos e treináveis no campo de machine learning e deep learning.
Em conclusão, o desdobramento detalhado da regra da cadeia aplicada a vetores e a correta distinção entre a derivada total e a derivada simples são fundamentais para a formação de pesquisadores e engenheiros que buscam excelência na criação e treinamento de redes neurais.
O próximo passo em pesquisa pode envolver a extensão destes conceitos para arquiteturas mais avançadas, como redes recorrentes e transformers, onde dependências temporais e estruturais complexas exigem ainda mais rigor matemático.
Fonte: (Towards Data Science – AI, ML & Deep Learning)



