São Paulo — InkDesign News — O avanço do machine learning e deep learning no cenário atual tem proporcionado uma nova perspectiva sobre a álgebra linear e suas aplicações em inteligência artificial. A compreensão dos conceitos fundamentais dessa disciplina é crucial para a implementação eficaz de algoritmos de aprendizado profundo.
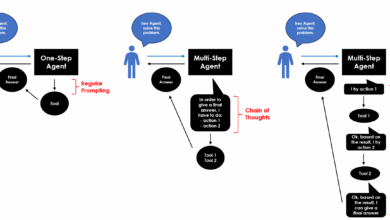
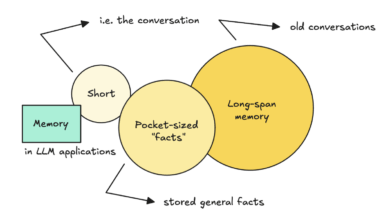
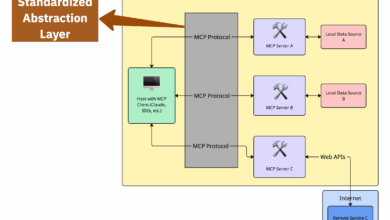
Arquitetura de modelo
O conceito de espaços vetoriais é essencial na construção de modelos de aprendizado. Todos os dados podem ser representados em um espaço vetorial, possibilitando que algoritmos mapeiem informações complexas, como imagens e linguagem. “No mundo da IA, a álgebra linear é a base para a manipulação de vetores de alta dimensão” (
“In the world of AI, linear algebra is the foundation for handling high-dimensional vectors”
— Autor Desconhecido
).
Treinamento e otimização
A aplicação de técnicas de mapas lineares desempenha um papel crucial no mapeamento de um vetor de entrada de um espaço a outro espaço vetorial, promovendo um aprendizado efetivo. O uso de matrizes para expressar esses mapas é comum, com a multiplicação de matrizes sendo um passo fundamental no processo. “É a multiplicação de matrizes que permite a transformação de dados de entrada em saídas significativas” (
“It’s matrix multiplication that enables the transformation of input data into meaningful outputs”
— Autor Desconhecido
).
Resultados e métricas
A performance dos modelos é frequentemente avaliada em termos de acurácia e tempo de treinamento. Modelos que incorporam conceitos de álgebra linear tendem a apresentar melhorias significativas em suas métricas de desempenho, especialmente ao lidar com conjuntos de dados complexos. Investigação em rank e determinantes de matrizes é vital para entender como maximizar a eficiência do modelo. “Explorar a rank de uma matriz permite que os pesquisadores determinem a dimensionalidade útil dos dados” (
“Exploring the rank of a matrix allows researchers to determine the useful dimensionality of the data”
— Autor Desconhecido
).
O potencial de aplicação dos conceitos de álgebra linear em problemas práticos de machine learning é vasto. Com a contínua evolução dos algoritmos, é evidente que novas pesquisas em álgebra linear poderão contribuir para avanços significativos em ciências computacionais e inteligência artificial.
Fonte: (Towards Data Science – AI, ML & Deep Learning)